I’m creating a graph of a small subset of train stations in the UK, and plan and am using dijkstra’s algorithm to find the most efficient path inbetween stations. I’ve always been interested in the algorithm’s that ticket selling websites use to calculate the fastest routes between stations on journeys that require various connections.

The Code

The code for creating the graph and dijkstra’s algorithm is below

Modelling as a graph

This problem can be easily modelled using a graph data structure using the adjacency list format.

Nodes are Stations

Each railway station on the graph can be represented as a Node object, holding a str value name and a dictionary services, of which keys are the destination station’s Node object and the value is the time the journey takes in minutes, represented as an int.

class Node:

  def __init__(self, name: str):
    self.name = name
    self.services = {}

  def add_service(self, station: Node, time: int):
    self.services[station] = time;

The add_service() function is used when constructing the graph, and creates a service to the destination station with given time

To keep the algorithm relatively fast to compute, I have selected a subset of railway stations in the UK. However, more stations can be added at any time later on.

# Locations from north to south, liv to eus
liv = Node("Liverpool Lime Street")
shf = Node("Sheffield")
sot = Node("Stoke on Trent")
bhm = Node("Birmingham New St")
lei = Node("Leicester")
nmp = Node("Northampton")
chm = Node("Cheltenham")
eus = Node("London Euston")

Edges are Services

I went on trainline and found example services between the stations on the graph. All of the times for each edge are accurate at the time of writing, and in the comments for the code I have made not of the operating company providing the service.

For the purpose of this example, it is assumed that all routes work both ways and take the same amount of time in either direction.

# Working up from south to north, eus to shf

# eus to bhm takes around 1hr 21mins (Avanti West Coast)
eus.add_service(bhm, 81)
bhm.add_service(eus, 81)
# eus to nmp takes around 55mins (West Midlands Trains)
eus.add_service(nmp, 55)
nmp.add_service(eus, 55)
# eus to liv takes around 2hr 20mins (Avanti West Coast)
eus.add_service(liv, 140)
liv.add_service(eus, 140)

# nmp to bhm takes around 1hr 4mins (West Midlands Trains)
nmp.add_service(bhm, 64)
bhm.add_service(nmp, 64)

# bhm to lei takes around 48mins (CrossCountry)
bhm.add_service(lei, 48)
lei.add_service(bhm, 48)
# bhm to shf takes around 1hr 5mins (CrossCountry)
bhm.add_service(shf, 65)
shf.add_service(bhm, 65)
# bhm to liv takes around 1hr 44mins (West Midlands Trains)
bhm.add_service(liv, 104)
liv.add_service(bhm, 104)
# bhm to sot takes around 52mins (West Midlands Trains)
bhm.add_service(sot, 52)
sot.add_service(bhm, 52)
# bhm to chm takes around 45min (CrossCountry)
bhm.add_service(chm, 45)
chm.add_service(bhm, 45)

# lei to shf is around 53mins (East Midlands Railway)
lei.add_service(shf, 53)
shf.add_service(lei, 53)

# shf to liv is around 1hr 45mins (East Midlands Railway)
shf.add_service(liv, 105)
liv.add_service(shf, 105)

Illustration

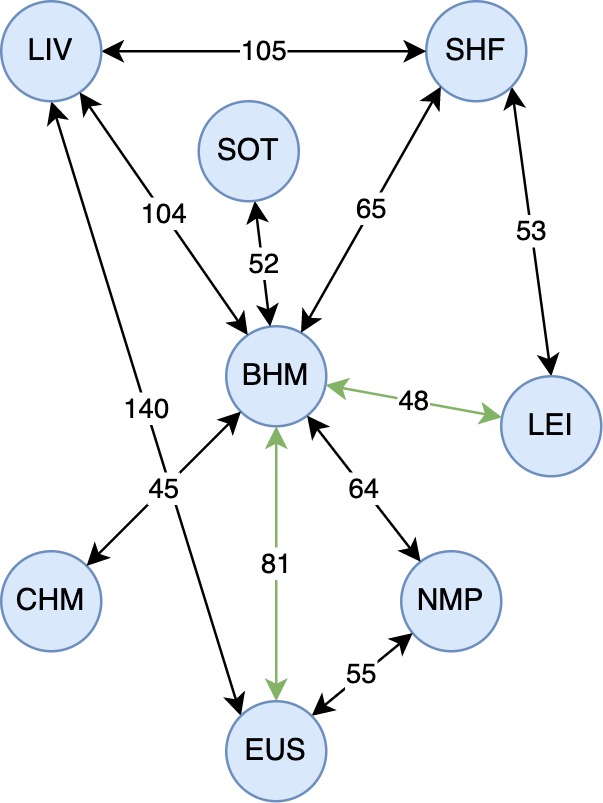
With all of the python code above, the following illustrated graph has been created consisting of the 8 stations and their inter-connecting services with time as the weights.

Shortest path with Dijkstra’s

I wanted to challenge myself by constructing Dijkstra’s algorithm completely on my own without any aid from resources on the internet. My approach was to follow the method I was taught at A-Level: producing a value table and holding the current lowest time to each node there, followed by it’s previous node.

So I am marking this section with a disclaimer, my solution is most definately not the most efficient, it’s merely the easiest for me to understand!

Recursively finding total time

In order to find the shortest known time to any given known location from the starting point, we need to recursively summate the time it takes to get to it’s previous node, and then it’s previous node …

The function get_time() implements this, taking the values dictionary, location and start values from the dijkstra function below.

def get_time(values, location, start):
  count = 0
  # If location has been visited before
  if location in values:
    count += values[location][0]
    # Recursively sum the time values
    if values[location][1] != start:
      count += get_time(values, values[location][1], start)

  return count

Dijkstra’s algorithm

The function dijkstra() performs Dijkstra’s algorithm on the graph starting from the start point, aiming to each the end point.

def dijkstra(start, end):

  # Start an array to hold the route
  route = []

  # Start a visited array
  visited = []

  # Start an empty values table
  values = {}

  # Initialise loop variables
  current = start

My implementation holds:

A list for the route found by the algorithm
The visited list of locations
The values table which stores a tuple representing the smallest time to the location and the node that shortest time is from. The total time from the start (used during calculating optimal time) can be recursively calcuated via the get_time() function

  # Loop until at the end
  while current != end:
    # Keep track of the smallest time
    smallest = None
    # For all services from the current point
    for service in current.services.items():
      to = service[0]
      time = service[1]
      # Skip services to locations already visited
      if to in visited: continue
      # Calculate the total distance to get to 'to'
      # if known (or 0)
      total = get_time(values, to, start)
      if get_time(values, current, start) + time <= total or total == 0:
        values[to] = (time, current)
      # Calculate the current value for the node
      # If no smallest, or the service is smaller
      if smallest == None or smallest[1] >= service[1]:
        # Smallest becomes the service
        smallest = service

    # Mark current as visited
    visited.append(current)

    # If smallest = None then every location
    # has been visited, so break from the loop
    if smallest == None:
      break

    # Move to the smallest
    current = smallest[0]

Now, outside of the first while loop the optimal route can be re-traced from the end to the start by following the previous value inside of the values table, until the starting value is reached.

These values are pushed to the beginning of the routes ‘stack’ to reverse the route into the correct order of steps. This can then be printed to the terminal with the for loop.


  # Start at the end and trace back
  current = end
  # Follow the shortest path from the table
  while True:
    route.insert(0, current)
    # Break from loop when end is reached
    if current == start:
      break
    # Trace back the route
    current = values[current][1]

  print("Route: ")
  for location in route:
    print(location.name)

Results

I have verified the funtionality of my implementation of the algorithm by running tests and comparing them to the logical route using the illustration of the graph.

Stoke on Trent -> Sheffield

dijkstra(sot, shf)

Stoke on Trent
Birmingham New Street
Sheffield

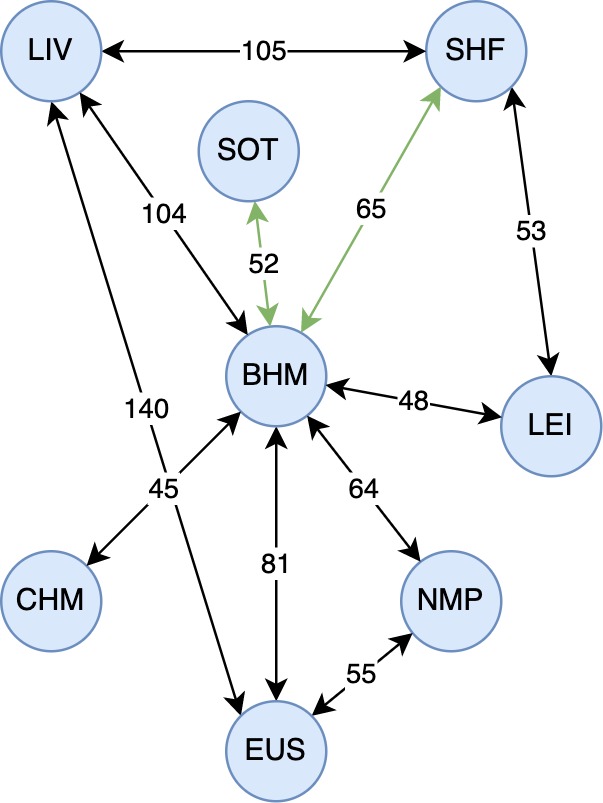
Liverpool Lime Street -> London Euston

dijkstra(liv, eus)

Liverpool Lime Street
London Euston

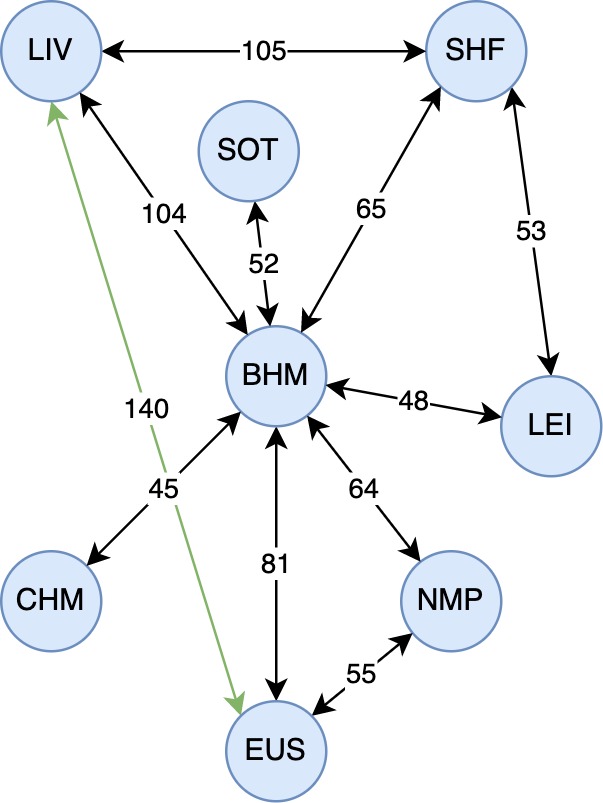
London Euston -> Leicester

dijkstra(eus, lei)

London Euston
Birmingham New Street
Leicester

Finding the optimal travel paths between a subset of UK railway stations using Dijkstra's algorithm